SQL групиране на интересни/припокриващи се редове

Ако приемем, че всички двойки съществуват и в тяхната огледална комбинация (4,5) и (5,4) . Но следните решения работят без огледални дупки също толкова добре.

Прост случай

Всички връзки могат да бъдат подредени в единична възходяща последователност и усложнения като тези, които добавих в цигулката не са възможни, можем да използваме това решение без дубликати в rCTE:

Започвам с получаване на минимум a_sno на група, с минималния свързан b_sno :

SELECT row_number() OVER (ORDER BY a_sno) AS grp
     , a_sno, min(b_sno) AS b_sno
FROM   data d
WHERE  a_sno < b_sno
AND    NOT EXISTS (
   SELECT 1 FROM data
   WHERE  b_sno = d.a_sno
   AND    a_sno < b_sno
   )
GROUP  BY a_sno;

Това изисква само едно ниво на заявка, тъй като прозоречна функция може да бъде изградена върху агрегат:

• Вземете отделната сума на колона на обединена таблица

Резултат:

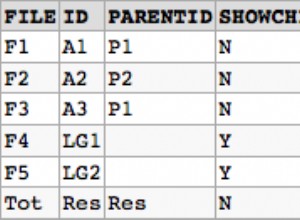
grp  a_sno  b_sno
1    4      5
2    9      10
3    11     15

Избягвам разклонения и дублирани (умножени) редове - потенциално много по-скъпи с дълги вериги. Използвам ORDER BY b_sno LIMIT 1 в корелирана подзаявка, за да накара това да лети в рекурсивен CTE.

• Създайте уникален индекс на неуникална колона

Ключът към производителността е съвпадащ индекс, който вече е наличен, предоставен от PK ограничението PRIMARY KEY (a_sno,b_sno) :не обратното (b_sno, a_sno) :

• Добър ли е съставният индекс и за заявки в първото поле?

WITH RECURSIVE t AS (
   SELECT row_number() OVER (ORDER BY d.a_sno) AS grp
        , a_sno, min(b_sno) AS b_sno  -- the smallest one
   FROM   data d
   WHERE  a_sno < b_sno
   AND    NOT EXISTS (
      SELECT 1 FROM data
      WHERE  b_sno = d.a_sno
      AND    a_sno < b_sno
      )
   GROUP  BY a_sno
   )

, cte AS (
   SELECT grp, b_sno AS sno FROM t

   UNION ALL
   SELECT c.grp
       , (SELECT b_sno  -- correlated subquery
          FROM   data
          WHERE  a_sno = c.sno
          AND    a_sno < b_sno
          ORDER  BY b_sno
          LIMIT  1)
   FROM   cte  c
   WHERE  c.sno IS NOT NULL
   )
SELECT * FROM cte
WHERE  sno IS NOT NULL   -- eliminate row with NULL
UNION  ALL               -- no duplicates
SELECT grp, a_sno FROM t
ORDER  BY grp, sno;

По-малко прост случай

Всички възли могат да бъдат достигнати във възходящ ред с едно или повече разклонения от корена (най-малкото sno ).

Този път вземете всички по-голямо sno и премахване на дублиращите се възли, които могат да бъдат посещавани многократно с UNION в края:

WITH RECURSIVE t AS (
   SELECT rank() OVER (ORDER BY d.a_sno) AS grp
        , a_sno, b_sno  -- get all rows for smallest a_sno
   FROM   data d
   WHERE  a_sno < b_sno
   AND    NOT EXISTS (
      SELECT 1 FROM data
      WHERE  b_sno = d.a_sno
      AND    a_sno < b_sno
      )
   )   
, cte AS (
   SELECT grp, b_sno AS sno FROM t

   UNION ALL
   SELECT c.grp, d.b_sno
   FROM   cte  c
   JOIN   data d ON d.a_sno = c.sno
                AND d.a_sno < d.b_sno  -- join to all connected rows
   )
SELECT grp, sno FROM cte
UNION                     -- eliminate duplicates
SELECT grp, a_sno FROM t  -- add first rows
ORDER  BY grp, sno;

За разлика от първото решение, тук не получаваме последен ред с NULL (причинен от корелираната подзаявка).

И двете трябва да се представят много добре - особено с дълги вериги / много разклонения. Резултат по желание:

SQL Fiddle (с добавени редове за демонстриране на трудността).

Неориентирана графика

Ако има локални минимуми, които не могат да бъдат достигнати от корена с възходящо преминаване, горните решения няма да работят. Помислете за решението на Farheg в този случай.