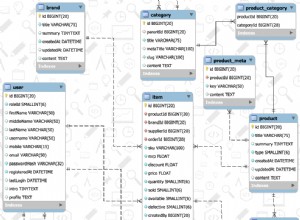
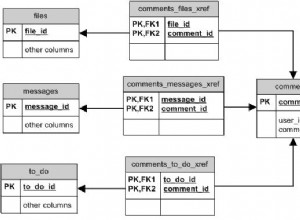
документация
е малко непълен по отношение на магията на стойността 6 и кога да приложите max функция, но ето таблица с моите констатации, базирана на тази документация.
Както се казва, формулите за деление са:
И както вие сами подчертавате, тогава имаме бележката под линия:
И така, ето какво създадох в моята електронна таблица:
p1 s1 p2 s2 prInit srInit prOver prAdjusted srAdjusted
38 16 38 16 93 55 55 38 6
28 16 28 16 73 45 35 38 10
29 16 29 16 75 46 37 38 9
И така, използвам pr и sr за указване на точността и мащаба на резултата. prInit и srInit формулите са точно форумите от документацията. Както виждаме, във всичките 3 случая точността на резултата е много по-голяма от 38 и така се прилага бележката под линия. prOver е просто max(0,prInit - 38) - с колко трябва да коригираме точността, ако се прилага бележката под линия. prAdjusted е просто prInit - prOver . Можем да видим и в трите случая, че крайната точност на резултата е 38 .
Ако приложа същото коефициент на корекция към скалите, тогава бих получил резултати от 0 , 10 и 9 . Но можем да видим, че вашият резултат за (38,16) case има скала 6 . Така че вярвам, че това е мястото, където max(6,... част от документацията действително се прилага. И така, последната ми формула за srAdjusted е max(6,srInit-prOver) и сега моят окончателен Adjusted изглежда, че стойностите съответстват на вашите резултати.
И, разбира се, ако се консултираме с документацията за decimal
, можем да видим, че по подразбиране прецизност и мащаб, ако не ги посочите, са (18,0) , така че ето реда за случаите, когато не сте посочили точност и мащаб:
p1 s1 p2 s2 prInit srInit prOver prAdjusted srAdjusted
18 0 18 0 37 19 0 37 19