Връщане на комбинации
Използвайки таблица с числа или CTE за генериране на числа, изберете 0 до 2^n - 1. Използвайки битовите позиции, съдържащи 1s в тези числа, за да посочите присъствието или отсъствието на относителните членове в комбинацията и елиминирането на тези, които нямат правилния брой стойности, трябва да можете да върнете набор от резултати с всички комбинации, които желаете.
WITH Nums (Num) AS ( SELECT Num FROM Numbers WHERE Num BETWEEN 0 AND POWER(2, @n) - 1), BaseSet AS ( SELECT ind =Power(2, Row_Number() OVER (ORDER BY) Стойност) - 1), * FROM @set), Combos AS ( SELECT ComboID =N.Num, S.Value, Cnt =Count(*) OVER (PARTITION BY N.Num) FROM Nums N INNER JOIN BaseSet S ON N. Num &S.ind <> 0)SELECT ComboID, ValueFROM CombosWHERE Cnt =@kORDER BY ComboID, Value; Тази заявка се представя доста добре, но се сетих за начин да я оптимизирам, като изпълня от Изящен паралелен брой битове първо да получите точния брой предмети, взети наведнъж. Това работи 3 до 3,5 пъти по-бързо (както CPU, така и време):
WITH Nums AS ( SELECT Num, P1 =(Num &0x55555555) + ((Num / 2) &0x55555555) FROM dbo.Numbers WHERE Num BETWEEN 0 AND POWER(2, @n) - 1), Nums2 AS ( SELECT Num, P2 =(P1 &0x33333333) + ((P1 / 4) &0x33333333) FROM Nums), Nums3 AS ( SELECT Num, P3 =(P2 &0x0f0f0f0f) + ((P2 / 16) &0x0f0f0f0f) FROM Nums2), BaseSet AS ( SELECT ind =Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM @set)SELECT ComboID =N.Num, S.ValueFROM Nums3 N INNER JOIN BaseSet S ON N .Num &S.ind <> 0WHERE P3 % 255 =@kORDER BY ComboID, стойност; Отидох и прочетох страницата за броене на битове и смятам, че това може да се представи по-добре, ако не направя % 255, а продължа докрай с битова аритметика. Когато имам възможност, ще го пробвам и ще видя как ще се справи.
Моите твърдения за производителност се основават на заявките, изпълнявани без клаузата ORDER BY. За по-голяма яснота това, което прави този код, е да брои броя на зададените 1-битове в Num от Числа маса. Това е така, защото числото се използва като вид индексатор за избор кои елементи от набора са в текущата комбинация, така че броят на 1-битовете ще бъде същият.
Надявам се да ви хареса!
За протокола, тази техника за използване на битовия модел на цели числа за избиране на членове на набор е това, което измислих „Вертикално кръстосано свързване“. Това ефективно води до кръстосано свързване на множество набори от данни, където броят на наборите и кръстосаните съединения е произволен. Тук броят на комплектите е броят елементи, взети наведнъж.
Всъщност кръстосаното свързване в обичайния хоризонтален смисъл (на добавяне на повече колони към съществуващия списък от колони с всяко свързване) би изглеждало по следния начин:
SELECT A.Value, B.Value, C.ValueFROM @Set A CROSS JOIN @Set B CROSS JOIN @Set CWHERE A.Value ='A' AND B.Value ='B' AND C.Value ='C' Моите запитвания по-горе ефективно „кръстосано свързване“ толкова пъти, колкото е необходимо, само с едно свързване. Резултатите не са завъртени в сравнение с действителните кръстосани съединения, разбира се, но това е незначителен въпрос.
Критика на вашия код
Първо, мога ли да предложа тази промяна във вашия Factorial UDF:
ALTER FUNCTION dbo.Factorial ( @x bigint)ВРЪЩА bigintASBEGIN IF @x <=1 RETURN 1 RETURN @x * dbo.Factorial(@x - 1)END
Сега можете да изчислявате много по-големи набори от комбинации, освен това е по-ефективно. Може дори да обмислите използването на decimal(38, 0) за да разрешите по-големи междинни изчисления във вашите комбинирани изчисления.
Второ, дадената от вас заявка не връща правилните резултати. Например, използвайки моите тестови данни от тестването на производителността по-долу, набор 1 е същият като набор 18. Изглежда, че вашата заявка приема плъзгаща се ивица, която се увива наоколо:всеки набор винаги е 5 съседни члена, изглеждащи нещо подобно (завъртях за по-лесно виждане):
<предварителен 1 ABCDE 2 ABCD Q 3 ABC PQ 4 AB OPQ 5 A NOPQ 6 MNOPQ 7 LMNOP 8 KLMNO 9 JKLMN 10 IJKLM 11 HIJKL 12 GHIJK 13 FGHIJ 14 EFGHI 15 DEFGH 16 CDEFG 17 BCDEF 18 ABCDE 19 ABCD Q
Сравнете модела от моите заявки:
31 ABCDE 47 ABCD F 55 ABC EF 59 AB DEF 61 A CDEF 62 BCDEF 79 ABCD G 87 ABC E G 91 AB DE G 93 A CDE G 94 BCDE G103 ABC FG107 AB D FG109 A CD FG110 BCD FG115 AB EFG117 A C EFG118 BC EFG121 A DEFG...
Само за да насоча битовия модел -> индекс на комбинацията вкъщи за всеки, който се интересува, забележете, че 31 в двоичен =11111 и моделът е ABCDE. 121 в двоичен код е 1111001 и моделът е A__DEFG (обратно картографиран).
Резултати от ефективността с таблица с реални числа
Проведох някои тестове за производителност с големи набори при второто ми запитване по-горе. В момента нямам запис за използваната версия на сървъра. Ето моите тестови данни:
DECLARE @k int, @n int;DECLARE @set TABLE (стойност varchar(24));INSERT @set VALUES ('A'),('B'),('C'),( 'D'), ('E'), ('F'), ('G'), ('H'), ('I'), ('J'), ('K'), ('L' '),('M'),('N'),('O'),('P'),('Q');SET @n =@@RowCount;SET @k =5;DECLARE @combinations bigint =dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));SELECT CAST(@combinations as varchar(max)) + 'combinations', MaxNumUsedFromNumbersTable =POWER (2, @n);
Питър показа, че това "вертикално кръстосано свързване" не работи толкова добре, колкото простото писане на динамичен SQL, за да направи действително CROSS JOINs, които избягва. С тривиалната цена на още няколко четения, неговото решение има показатели между 10 и 17 пъти по-добри. Производителността на неговата заявка намалява по-бързо от моята с увеличаване на обема на работа, но не достатъчно бързо, за да спре някой да я използва.
Вторият набор от числа по-долу е коефициентът, разделен на първия ред в таблицата, само за да покаже как се мащабира.
Ерик
Елементи CPU Записва Четене Продължителност | CPU записва чете Продължителност----- ------ ------ ------- -------- | ----- ------ ------ --------17•5 7344 0 3861 8531 |18•9 17141 0 7748 18536 | 2.3 2.0 2.220•10 76657 0 34078 84614 | 10,4 8,8 9,921•11 163859 0 73426 176969 | 22,3 19,0 20,721•20 142172 0 71198 154441 | 19.4 18.4 18.1
Петър
Елементи CPU Записва Четене Продължителност | CPU записва чете Продължителност----- ------ ------ ------- -------- | ----- ------ ------ --------17•5 422 70 10263 794 | 18•9 6046 980 219180 11148 | 14,3 14,0 21,4 14,020•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.121•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.321•20 51391 5 6291273 55169 | 121,8 0,1 613,0 69,5
Екстраполирайки, в крайна сметка моята заявка ще бъде по-евтина (въпреки че е от самото начало в четения), но не и за дълго време. За да използвате 21 елемента в комплекта, вече е необходима таблица с числа до 2097152...
Ето един коментар, който първоначално направих, преди да разбера, че решението ми ще се представи драстично по-добре с таблица с числа в движение:
Резултати от производителността с таблица с числа в движение
Когато първоначално написах този отговор, казах:
Е, опитах го и резултатите бяха, че се представи много по-добре! Ето заявката, която използвах:
DECLARE @N int =16, @K int =12;CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);CREATE TABLE #Items (Num int);INSERT #Items VALUES (@K );INSERT #Set SELECT TOP (@N) VFROM (VALUES ('A'),('B'),('C'),('D'),('E'),('F'), ('G'), ('H'), ('I'), ('J'), ('K'), ('L'), ('M'), ('N'), (' O'), ('P'), ('Q'), ('R'), ('S'), ('T'), ('U'), ('V'), ('W' ),('X'),('Y'),('Z')) X (V);GODECLARE @N int =(SELECT Count(*) FROM #Set), @K int =(SELECT TOP 1 Num FROM #Items);DECLARE @combination int, @value char(1);WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),L1 AS (SELECT 1 N FROM L0, L0 B),L2 AS (SELECT 1 N FROM L1, L1 B),L3 AS (ИЗБЕРЕТЕ 1 N ОТ L2, L2 B),L4 AS (ИЗБЕРЕТЕ 1 N ОТ L3, L3 B),L5 AS (ИЗБЕРЕТЕ 1 N ОТ L4, L4 B),Nums AS (ИЗБЕРЕТЕ номер_на_ред) () OVER(ORDER BY (SELECT 1)) Num FROM L5),Nums1 AS ( SELECT Num, P1 =(Num &0x55555555) + ((Num / 2) &0x55555555) FROM Nums WHERE Num BETWEEN 0 AND Power(2, @N) - 1), Nums2 AS ( SELECT Num, P2 =(P1 &0x33333333) + ((P1 / 4) &0x33333333) FROM Nums1), Nums3 AS ( SELECT Num, P3 =(P2 &0x0F0F0F0F) + ((P2 / 16) &0x0F0F0F0F) FROM Nums2), BaseSet AS ( SELECT Ind =Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)SELECT @Combination =N.Num, @Value =S.ValueFROM Nums3 N INNER JOIN BaseSet S ON N.Num &S.Ind <> 0WHERE P3 % 255 =@K;
Имайте предвид, че избрах стойностите в променливи, за да намаля времето и паметта, необходими за тестване на всичко. Сървърът все още върши същата работа. Модифицирах версията на Питър, за да бъде подобна, и премахнах ненужните екстри, така че и двете да са възможно най-слаби. Версията на сървъра, използвана за тези тестове, е Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition на Windows NT 5.2 (Компилация 3790:Service Pack 2) (VM) работи на виртуална машина.
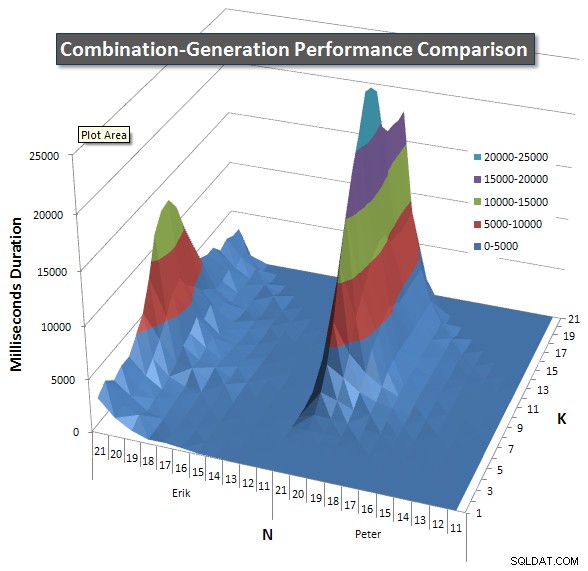
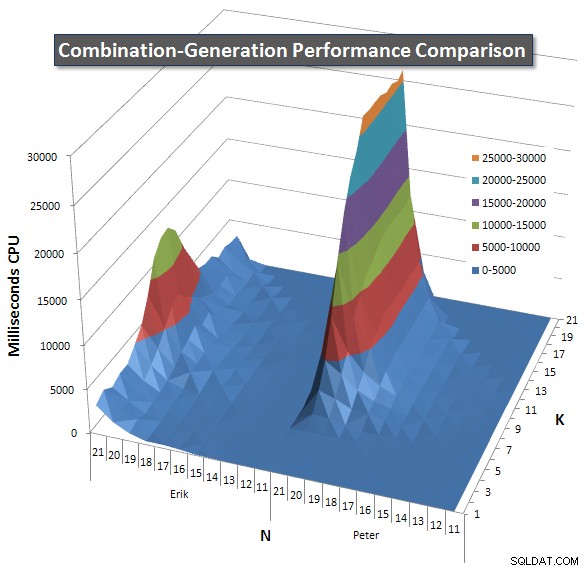
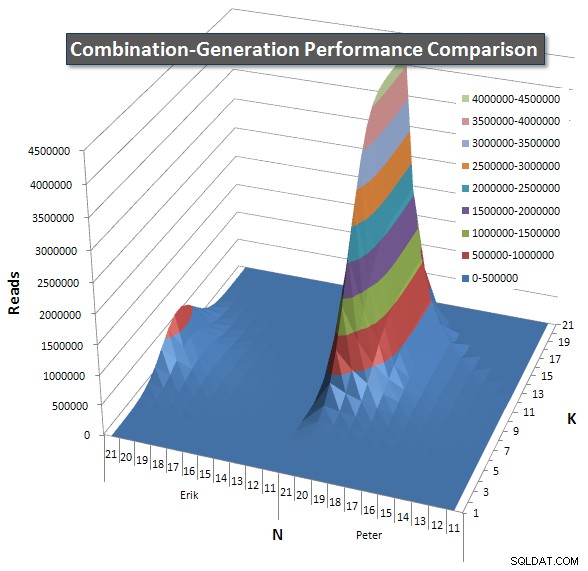
По-долу има диаграми, показващи кривите на производителност за стойности на N и K до 21. Базовите данни за тях са в друг отговор на тази страница
. Стойностите са резултат от 5 изпълнения на всяка заявка при всяка стойност на K и N, последвано от изхвърляне на най-добрите и най-лошите стойности за всеки показател и осредняване на останалите 3.
По принцип моята версия има „рамо“ (в най-левия ъгъл на диаграмата) при високи стойности на N и ниски стойности на K, което я прави по-лоша там от версията на динамичния SQL. Това обаче остава сравнително ниско и постоянно и централният пик около N =21 и K =11 е много по-нисък за продължителност, процесор и четения в сравнение с динамичната SQL версия.
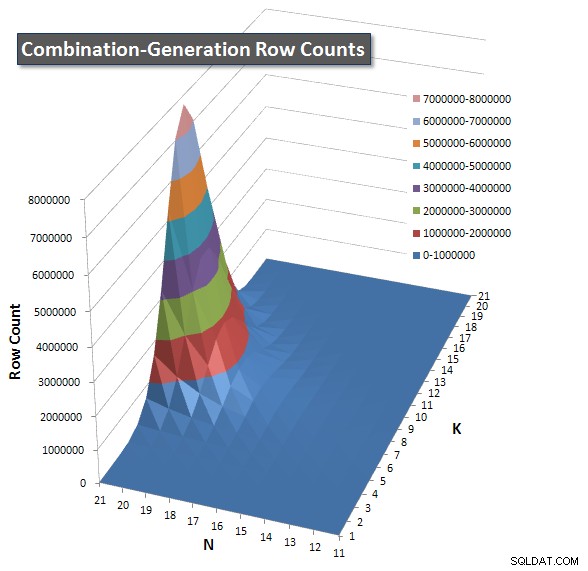
Включих диаграма на броя редове, които се очаква да върне всеки елемент, така че можете да видите как се представя заявката спрямо това колко голяма работа трябва да свърши.
Моля, вижте допълнителния ми отговор на тази страница
за пълни резултати от изпълнението. Достигнах ограничението за знаци в публикацията и не можах да я включа тук. (Някакви идеи къде другаде да го поставя?) За да поставя нещата в перспектива спрямо резултатите от производителността на първата ми версия, ето същия формат като преди:
Ерик
Елементи CPU Продължителност Четене Запис | CPU Duration Reads ----- ----- -------- ------- ------ | ----- -------- -------17•5 354 378 12382 0 |18•9 1849 1893 97246 0 | 5,2 5,0 7,920•10 7119 7357 369518 0 | 20,1 19,5 29,821•11 13531 13807 705438 0 | 38,2 36,5 57,021•20 3234 3295 48 0 | 9,1 8,7 0,0
Петър
Елементи CPU Продължителност Четене Запис | CPU Duration Reads ----- ----- -------- ------- ------ | ----- -------- -------17•5 41 45 6433 0 | 18•9 2051 1522 214021 0 | 50.0 33.8 33.320•10 8271 6685 864455 0 | 201.7 148.6 134.421•11 18823 15502 2097909 0 | 459.1 344.5 326.121•20 25688 17653 4195863 0 | 626,5 392,3 652,2
Изводи
- Таблиците с числа в движение са по-добри от истинска таблица, съдържаща редове, тъй като четенето на една при огромен брой редове изисква много I/O. По-добре е да използвате малко CPU.
- Първоначалните ми тестове не бяха достатъчно широки, за да покажат наистина характеристиките на производителността на двете версии.
- Версията на Питър може да бъде подобрена, като всяко JOIN не само бъде по-голямо от предишния елемент, но също така ограничи максималната стойност въз основа на това колко повече елемента трябва да се поберат в комплекта. Например, при 21 елемента, взети по 21 наведнъж, има само един отговор от 21 реда (всичките 21 елемента, еднократно), но междинните набори редове в динамичната SQL версия, в началото на плана за изпълнение, съдържат комбинации като " AU" на стъпка 2, въпреки че това ще бъде отхвърлено при следващото присъединяване, тъй като няма налична стойност, по-висока от "U". По същия начин, междинен набор от редове в стъпка 5 ще съдържа "ARSTU", но единствената валидна комбинация в този момент е "ABCDE". Тази подобрена версия няма да има по-нисък пик в центъра, така че вероятно няма да я подобри достатъчно, за да стане ясен победител, но поне ще стане симетрична, така че диаграмите да не остават максимизирани след средата на региона, а ще се върнат назад до почти 0, както прави моята версия (вижте горния ъгъл на пиковете за всяка заявка).
Анализ на продължителност
- Няма наистина значителна разлика между версиите в продължителността (>100ms) до 14 елемента, взети по 12 наведнъж. До този момент моята версия печели 30 пъти, а динамичната SQL версия печели 43 пъти.
- Започвайки от 14•12, моята версия беше по-бърза 65 пъти (59>100ms), динамичната SQL версия 64 пъти (60>100ms). Въпреки това, винаги когато моята версия беше по-бърза, тя спести общо средно времетраене от 256,5 секунди, а когато динамичната SQL версия беше по-бърза, спести 80,2 секунди.
- Общата средна продължителност за всички опити е Ерик 270,3 секунди, Питър 446,2 секунди.
- Ако беше създадена справочна таблица, за да се определи коя версия да се използва (като се избере по-бързата за входовете), всички резултати биха могли да бъдат изпълнени за 188,7 секунди. Използването на най-бавния всеки път ще отнеме 527,7 секунди.
Чете анализ
Анализът на продължителността показа, че моята заявка печели със значително, но не прекалено голямо количество. Когато показателят се превключи на четения, се появява много различна картина - моята заявка използва средно 1/10 от четенията.
- Няма наистина значителна разлика между версиите в четенията (>1000) до 9 елемента, взети по 9 наведнъж. До този момент моята версия печели 30 пъти, а динамичната SQL версия печели 17 пъти.
- Започвайки от 9•9, моята версия използва по-малко четения 118 пъти (113>1000), динамичната SQL версия 69 пъти (31>1000). Въпреки това, винаги когато моята версия е използвала по-малко четения, тя е спестила средно 75,9 милиона четения, а когато динамичната SQL версия е била по-бърза, тя е спестила 380 000 четения.
- Общото осреднено четене за всички опити беше Ерик 8,4 милиона, Питър 84 милиона.
- Ако беше създадена справочна таблица, за да се определи коя версия да се използва (избиране на най-добрата за входовете), всички резултати могат да бъдат извършени в 8 милиона четения. Използването на най-лошия всеки път ще отнеме 84,3 милиона прочитания.
Ще ми бъде много интересно да видя резултатите от актуализирана динамична версия на SQL, която поставя допълнителната горна граница на елементите, избрани на всяка стъпка, както описах по-горе.
Допълнение
Следната версия на моята заявка постига подобрение от около 2,25% в сравнение с резултатите за производителност, изброени по-горе. Използвах метода за броене на битове HAKMEM на MIT и добавих Convert(int) върху резултата от row_number() тъй като връща bigint. Разбира се, бих искал това да е версията, с която бях използвал за всички тестове за производителност и диаграми и данни по-горе, но е малко вероятно някога да я повторя, тъй като беше трудоемко.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),L1 AS (SELECT 1 N FROM L0, L0 B),L2 AS (SELECT 1 N FROM L1, L1 B),L3 AS (SELECT 1 N ОТ L2, L2 B),L4 AS (ИЗБЕРЕТЕ 1 N ОТ L3, L3 B),L5 AS (ИЗБЕРЕТЕ 1 N ОТ L4, L4 B),Nums AS (ИЗБЕРЕТЕ Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),Nums1 AS ( SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1), Nums2 AS ( SELECT Num, P1 =Num - ((Num / 2) &0xDB6DB6DB) - ((Num / 4) &0x49249249) FROM Nums1), Nums3 AS (SELECT Num, Bits =((P1 + P1 / 8) &0xC71C71C7) % 63 FROM Nums2), BaseSet AS (SELECT Ind =Power( 2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)SELECT N.Num, S.ValueFROM Nums3 N INNER JOIN BaseSet S ON N.Num &S.Ind <> 0WHERE Bits =@K
И не можах да устоя да покажа още една версия, която прави търсене, за да получи броя на битовете. Може дори да е по-бързо от други версии:
DECLARE @BitCounts binary(255) =0x01010201020203010202030203030401020203020303040203030403040405 + 0x0102020302030304020303040304040502030304030404050304040504050506 + 0x0102020302030304020303040304040502030304030404050304040504050506 + 0x0203030403040405030404050405050603040405040505060405050605060607 + 0x0102020302030304020303040304040502030304030404050304040504050506 + 0x0203030403040405030404050405050603040405040505060405050605060607 + 0x0203030403040405030404050405050603040405040505060405050605060607 + 0x0304040504050506040505060506060704050506050606070506060706070708;WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),L1 AS (SELECT 1 N FROM L0, L0 B),L2 AS (ИЗБЕРЕТЕ 1 N ОТ L1, L1 B),L3 AS (ИЗБЕРЕТЕ 1 N ОТ L2, L2 B),L4 AS (ИЗБЕРЕТЕ 1 N ОТ L3, L3 B),L5 AS (ИЗБЕРЕТЕ 1 N FROM L4, L4 B),Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2) , @N) - 1), BaseSet AS (SELECT Ind =Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)SELECT @Combination =N.Num, @Value =S.ValueFROM Nums1 N INNER JOIN BaseSet S ON N.Num &S.Ind <> 0WHERE @K =Преобразуване(int, Substring(@BitCounts, N.Num &0xFF, 1)) + Convert(int, Substring(@BitCounts, N.Num / 256 &0xFF, 1)) + Convert(int, Substring (@BitCounts, N.Num / 65536 &0xFF, 1)) + Преобразуване(int, Substring(@BitCounts, N.Num / 16777216, 1))