Ако търсите алгоритъм за апроксимация, предлагам да потърсите алгоритъм на k-средни или йерархичен клъстер, особено крива на чудовище или крива за запълване на пространство. Първо можете да изчислите минимално обхващащо дърво на графиката и след това да премахнете най-дългите и най-скъпите ръбове. Тогава дървото прави много малки дървета и можете да използвате k-средните, за да изчислите група от точки, т.е. клъстери.
"Алгоритъмът за k-клъстериране с една връзка... е точно алгоритъмът на Крускал... еквивалентен на намиране на MST и изтриване на k-1 най-скъпите ръбове." Вижте например тук:https://stats.stackexchange.com/ questions/1475/visualization-software-for-clustering .
Добър пример за чудовищна крива е кривата на хилберт. Основната форма на тази крива е U-образна форма и чрез копиране на много от нея заедно и завъртането й кривата запълва еуклидийното пространство. Изненадващо сив код може да ви помогне да разберете ориентацията на тази U-образна форма. Можете да потърсите кривата на quadtree на Хилбърт на Ник статия в блога за повече подробности . Вместо да изчислите индекса на кривата, можете да съберете quadkey като в bing карти. Квадроключът е уникален за всяка координата и може да се използва с нормални низови операции. Всяка позиция в клавиша е част от U-образната крива и по този начин можете да изберете този регион от точки от избор частично отляво надясно от клавиша quad.
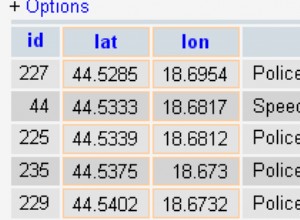
На това изображение можете да видите, че зеленият многоъгълник се намира с помощта на крива на Хилберт:
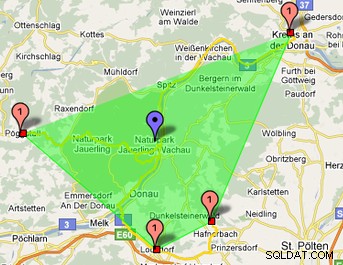
Можете да намерите моите php класове тук:https://www.phpclasses.org/package/6202-PHP-Generate-points-of-an-Hilbert-curve.html