Как да съхранявате двупосочни връзки в RDBMS като MySQL?

Ето как тези два подхода ще бъдат физически представени в базата данни:

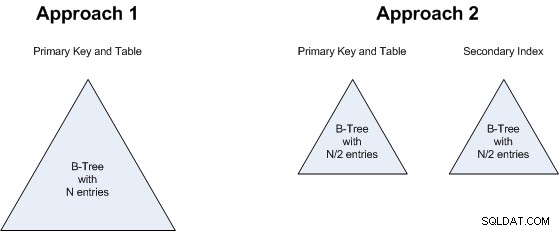
Нека анализираме и двата подхода...

Подход 1 (и двете посоки са записани в таблицата):

• ПРО:По-прости заявки.
• CON:Данните могат да бъдат повредени чрез вмъкване/актуализиране/изтриване само една посока.
• MINOR PRO:Не изисква допълнителни ограничения, за да се гарантира, че приятелството не може да бъде дублирано.
• Необходим е допълнителен анализ:
  1. TIE:Един индекс корици и в двете посоки, така че нямате нужда от вторичен индекс.
  2. TIE:Изисквания за съхранение.
  3. TIE:Изпълнение.

Подход 2 (само една посока, съхранена в таблицата):

• CON:По-сложни заявки.
• ПРО:Данните не могат да бъдат повредени, като забравите да обработвате обратната посока, тъй като няма противоположна посока .
• НЕМАЛКО ПРОТИВО:Изисква CHECK(UID < FriendID) , така че едно и също приятелство никога не може да бъде представено по два различни начина, а ключът на (UID, FriendID) може да си свърши работата.
• Необходим е допълнителен анализ:
  1. TIE:Необходими са два индекса за покриване и двете посоки на заявка (съставен индекс на {UID, FriendID} и съставен индекс на {FriendID, UID} ).
  2. TIE:Изисквания за съхранение.
  3. TIE:Изпълнение.

Вточка 1 представлява особен интерес. MySQL/InnoDB винаги клъстери данни, а вторичните индекси могат да бъдат скъпи в клъстерирани таблици (вижте "Недостатъци на клъстерирането" в тази статия ), така че може да изглежда така, сякаш вторичният индекс в подход 2 ще изяде всички предимства на по-малко редове. Въпреки това , вторичният индекс съдържа точно същите полета като основния (само в обратния ред), така че в този конкретен случай няма излишни разходи за съхранение. Освен това няма указател към таблици (тъй като няма таблична купчина), така че вероятно е дори по-евтино от гледна точка на съхранение, отколкото обикновен индекс, базиран на heap. И ако приемем, че заявката е покрита с индекса, няма да има двойно търсене, обикновено свързано с вторичен индекс в клъстерирана таблица. Така че по същество това е равенство (нито подход 1, нито подход 2 имат значително предимство).

Вточка 2 е свързано с точка 1:няма значение дали ще имаме B-дърво от N стойности или две B-дървета, всяко с N/2 стойности. Така че това също е равенство:и двата подхода ще изразходват приблизително същото количество място за съхранение.

Същите аргументи важи и за точка 3 :дали търсим едно по-голямо B-дърво или 2 по-малки, няма голяма разлика, така че това също е равен.

Така че, за здравината и въпреки малко по-грозните заявки и необходимостта от допълнителна CHECK , аз бих използвал подход 2.