За да решите това, трябва да разберете уравнението на окръжността, което е нещо подобно. За всяка точка (x,y) да попада в окръжност с център (x1, y1) и радиус r единици е
(x-x1)^2 + (y - y1)^2 <= r^2
where a^b = a to the power b
Тук във вашия случай потребители Б (географска ширина, дължина) са центъра на кръга, потребители А (ширина, дължина) са точките (x,y) и радиус =2 км.
Но основният проблем е смяната на градуси от географски ширини към дължини, така че ето решението, 1 градус =111,12 км. Така че, за да запазим единиците еднакви от двете страни на уравнението, ще ги преобразуваме в Kms
Така че нашето окончателно уравнение става:
((x-x1)*111.12)^2 + ((y-y1)*111.12)^2 = 4 (=2^2)
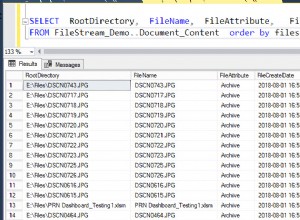
SQL изразът за същото трябва да изглежда така
SELECT A.user_id, A.radius_id, A.latitude, A.logitude
FROM UserA AS A,
(SELECT user_id, latitude, longitude
FROM UserB
WHERE user_id = 8) AS B
WHERE (POW((A.latitude-B.latitude)*111.12, 2) + POW((A.longitude - B.longitude)*111.12, 2)) <= 4
/* **Edit** Here I have used (A.longitude - B.longitude)*111.12, for more accurate results one can replace it with (A.longitude - B.longitude)*111.12*cos(A.latitude)) or (A.longitude - B.longitude)*111.12*cos(B.latitude))
And, as i have suggested in the comments that first filter some records based on approximation, so whether one uses A.latitude or B.latitude it will not make much difference */
Надявам се това да помогне...